MATEMATICA II 3º FISICO MATEMATICO - MATEMATICA III 3º SOCIAL ECONOMIA

MATEMATICA II: 3º FISICO MATEMÁTICA (Reformulación 2006)
MATEMATICA III: 3º SOCIAL ECONOMÍA (Reformulación 2006)

APLICACIONES DE LA ELIPSE

1- ¿QUÉ ES LA LITOTRICIA?
Se trata de un método no invasivo, que parte los cálculos del riñón o de la vía urinaria, en fragmentos más pequeños, para que sean eliminados por el propio organismo.Consiste en un método en el cual se generan unas ondas por fuera del cuerpo, posteriormente se dirigen al cálculo ubicado, ya sea por rayos X o por ultrasonido, las ondas de choque son generadas por una chispa, descargada bajo el agua, y un electrodo ( Bujía ) localizada dentro del reflector de una elipse(campana). Debido a esta forma de elipse o campana, al generar la chispa, todas las ondas se dirigen al cálculo, con una muy alta densidad, entonces el cálculo se fragmenta.

Desde hace veinticinco años, el tratamiento de los cálculos o “piedras” localizada en las vías urinarias, ha avanzado considerablemente. Antes era necesario realizar una cirugía mayor para extraer un pequeño cálculo, mientras que en la actualidad, sólo es necesario operar a menos del 5% de los pacientes que sufren este padecimiento y esto se debe a que, generalmente, el paciente presenta daño renal.

Existen dos formas de llevar a cabo la litotricia:

2- ¿CÓMO ACTÚAN LAS ONDAS DE CHOQUE?

Las ondas de choque consisten en un frente de presión positiva de múltiples frecuencias con un pico inmediato y un descenso gradual. A este respecto, el uso de las ondas de choque para la destrucción de cálculos renales se basa, entre otras, en las siguientes propiedades:

Cuando golpean un material quebradizo, como un cálculo renal, las ondas de choque crean un elevado gradiente de presión que causa su destrucción.

La intensidad necesaria para destruir cálculos debe ser inferior al nivel de tolerancia de los tejidos celulares, con el fin de que sólo afecte a los primeros.

Las ondas de choque pueden ser transmitidas libremente y propagadas a través del cuerpo sin originar una importante pérdida de energía cuando se usa el agua como medio de transmisión.

Además, pueden ser enfocadas con precisión si se integran en un sistema reflector apropiado (con forma de elipse).

3. LITOTRICIA RENAL EXTRACORPÓREA POR ONDAS DE CHOQUE: EL FUNCIONAMIENTO
Los litotriptores son aparatos que cuentan con un generador electromagnético que produce una onda de choque de grandes amplitudes en un foco, localizado geométricamente con rayos x.

La transmisión de las ondas de choque en medios de escasa reflexión (agua y tejidos corporales que la contienen en abundancia) no sufre casi pérdidas. Su velocidad de propagación se aproxima a la del sonido en el agua.

Al llegar la onda de choque focalizada, a zonas de densidad diferente a la del contorno (cálculos), libera en ellas energía mecánica. Éste es el fundamento de la destrucción de los cálculos mediante litotricia extracorpórea.

Descripción del procedimiento

1) El paciente es colocado en una superficie horizontal (mesa de emplazamiento).

2) Se monitorizan informáticamente los signos vitales del paciente a lo largo de todo el procedimiento: presión arterial, electrocardiograma, etc.

3) Localización del cálculo mediante un sistema radiológico de exploración. La imagen se visualiza con gran definición para lograr un enfoque preciso y milimétrico.

4) Se acopla el aplicador de ondas de choque al cuerpo del paciente y se inicia la sesión. La intensidad y duración de las ondas se controlan informáticamente, según el tamaño de los cálculos.

5) En el punto focal, previamente localizado, se descarga la onda de choque.

6) Finalmente, se comprueba por medio de una placa radiológica que los cálculos hayan sido destruidos.

http://www.wipo.int/pctdb/en/wo.jsp?IA=MX1995000008&DISPLAY=DESC

REFLECTORES MULTIFOCALES COMPUESTOS PARA CONCENTRAR ONDAS DE CHOQUE
Campo de la Invención
La presente invención se refiere a reflectores multifocales compuestos hechos por segmentos cuya forma es la de sectores y/o anillos de elipsoides de revolución que pueden ser truncados a la misma o a diferentes alturas con las mismas o diferentes distancias entre focos, o bien, con las mismas o diferentes longitudes de los semiejes de cada uno de los segmentos que conforman a dichos reflectores, pudiéndose dar el caso de que con la unión de más de tres segmentos para formar al reflector, algunos segmentos sean iguales, o bien, que con la unión de más de dos segmentos, algunos provengan del mismo elipsoide de revolución. Obviamente, si el reflector está formado únicamente por segmentos anulares o anillos, el reflector multifocal compuesto resultante será simétrico con respecto al eje de simetría de los segmentos que lo componen. Dichos reflectores multifocales compuestos, sectoriales o anulares, sirven por ejemplo, para concentrar ondas de choque producidas por dispositivos que actualmente emplean reflectores con forma de elipsoides de revolución para concentrarlas, lo que posibilita, entre otras aplicaciones, la desintegración más eficiente de ciertos objetos frágiles, como por ejemplo los cálculos renales, es decir, al usar los reflectores multifocales compuestos en los equipos clínicos de litotripsia extracorporal existentes, se podrían fracturar con un menor número de ondas de choque. Antecedentes de la Invención
En el año de 1980, en Munich, Alemania, se practicó la primera litotripsia extracorporal (también denominada litotricia extracorpórea) por ondas de choque, esto es, desintegración de cálculos renales con un método no invasivo. Actualmente existen varias compañías que ofrecen litotriptores (también denominados litotriptores) extracorporales, nombre que se da a los aparatos que pulverizan cálculos renales o biliares con ondas de choque. La idea fundamental es generar ondas de choque fuera del cuerpo humano, hacerlas pasar por él con un mínimo de pérdidas de energía y concentrarlas sobre el cálculo, creando con ello, una serie de esfuerzos que originan la ruptura del cálculo en varios fragmentos pequeños, que posteriormente puedan ser eliminados por el paciente. Hoy en día, hay en el mundo más de un millar de litotriptores extracorporales para desintegrar cálculos renales, biliares e incluso salivales. Existen litotriptores extracorporales que generan ondas de choque por diferentes métodos, como el electrohidráulico, el electroconductivo, el electromagnético, el piezoeléctrico y el de microexplosivos.
En los dispositivos electrohidráulicos y en los electroconductivos, por ejemplo, se generan descargas eléctricas de alto voltaje (decenas de miles de voltios) entre dos electrodos sumergidos en agua u otro líquido adecuado, lo cual forma un pequeño canal de agua evaporada o de algún otro líquido también evaporado (plasma) que se expande súbitamente, comprimiendo el medio circundante en forma semejante a lo que ocurre en la explosión de una bomba. Esto genera una onda de compresión que después de propagarse unos cuantos centímetros en el agua se transforma en una onda de choque, que es una discontinuidad de presión que se propaga como onda esférica por el medio. Los litotriptores microexplosivos usan pequeñas cargas explosivas para producir el mismo efecto.
En los litotriptores electrohidráulicos, electroconductivos y microexplosivos, una componente importante es el reflector con geometría de elipsoide de revolución truncado. Este reflector puede estar hecho de latón o de algún otro material con propiedades mecánicas similares. Su función es concentrar en el segundo foco (F2) las ondas de choque generadas en el primer foco (Fl) del elipsoide de revolución, o sea en el foco más cercano al reflector, lo cual genera una región de máxima energía en la vecindad del segundo foco (F2) o sea en el foco más lejano a la superficie interna del reflector.
El segundo foco, en el que no se generan las ondas, deberá coincidir con el objeto que se desee desintegrar, como por ejemplo un cálculo renal. En los equipos clínicos de litotripsia extracorporal, la coincidencia del objeto con el segundo foco del elipsoide se logra por medio de un sistema de fluoroscopía y/o por medio de un equipo de ultrasonido.
-->A la fecha todos los litotriptores electrohidráulicos, los electroconductivos y los de microexplosivos usan reflectores en forma de elipsoides de revolución truncados en uno de sus extremos. La simetría de revolución de estos reflectores es con respecto al eje mayor del elipsoide.
En los reflectores convencionales con forma de elipsdoide de revolución, las ondas de choque generadas en el primer foco (Fl) , se concentran necesariamente en fase, temporal y espacial, en el segundo foco (F2) . Esto, como se verá, es una limitante.
Es por lo tanto objeto de la presente invención proporcionar un nuevo arreglo, llamado reflector multifocal compuesto, con la característica de que está formado por segmentos de elipsoides de revolución, con las mismas o diferentes longitudes de los semiejes y con las mismas o diferentes distancias focales de cada uno de los segmentos de elipsoides de revolución.
-->Otro objeto de la presente invención es proporcionar un arreglo novedoso en el que al generarse ondas de choque en el reflector multifocal compuesto, estas ondas se desfasan tanto en el espacio como en el tiempo, generando con ésto, torcas y esfuerzos en cualquier objeto colocado en el sitio indicado (F2, F2 ' , F2 '', ...) , con lo que se obtiene una mayor eficiencia para desintegrarlos.

MATEMATICA II 3º FISICO MATEMATICO - MATEMATICA III 3º SOCIAL ECONOMIA

MATEMATICA II: 3º FISICO MATEMÁTICA (Reformulación 2006)
MATEMATICA III: 3º SOCIAL ECONOMÍA (Reformulación 2006)
APLICACIONES DE LA PARÁBOLA: MOVIMIENTO DE PROYECTILES


Consideremos un proyectil disparado en el vacío con una velocidad inicial v0 , bajo un ángulo de tiro α.

Para determinar la trayectoria de este proyectil tomemos un sistema de ejes cartesianos ortogonales situado en el plano vertical que contiene al eje del arma, que tenga por origen la posición inicial del centro del proyectil, y en el que el eje OX sea horizontal. En este plano se mueve dicho centro.
Para encontrar la posición del proyectil, t segundos después del disparo, aplicamos el principio de independencia de los movimientos.




De acuerdo con él podemos suponer descompuesto el movimiento real del proyectil en otros dos. Uno uniforme, de velocidad vo, según la dirección del eje del arma, y otro, uniformemente acelerado, de caída. Al cabo de t segundos el proyectil se encontraría en A a la distancia v0 t de su posición inicial, si obedeciese únicamente al primer movimiento, pero como simultáneamente va cayendo, durante t segundos recorrerá hacia abajo una distancia vertical ½ .g.t2 , siendo g la aceleración de la gravedad en el lugar en que se efectúa el disparo.
Por lo tanto la posición del proyectil, t segundos después del disparo se obtiene componiendo esos movimientos con lo que se determina el punto P. Las coordenadas de este punto P(x;y) que es uno cualquiera de la trayectoria del proyectil son:
y constituyen así las ecuaciones paramétricas de la trayectoria del proyectil. Para hallar su ecuación cartesiana ordinaria debemos eliminar el parámetro t entre ambas ecuaciones. Para ello despejamos t en (1) y lo sustituimos en (2):
De (1) resulta:

lo que nos indica que: La trayectoria de un proyectil disparado en el vacío es una parábola de eje vertical.
Para hallar el vértice sacamos a de factor común:

Si queremos hallar el alcance máximo de ese tiro hallamos el valor de x para el cual es y=0, es decir, la abcisa del punto en que vuelve a tierra el proyectil.

valor éste que es igual al duplo de la abcisa del vértice de la parábola. Esta particularidad no debe extrañarnos, puesto que, por ser, en este caso, el eje de la parábola paralelo al eje OY, el punto de caída del proyectil debe ser simétrico con respecto a ese eje del punto de partida, de donde resulta que la distancia entre ambos debe ser el doble de la distancia del primero al eje; y como el punto de partida coincide con el origen, esas distancias son sus respectivas abcisas.

MATEMATICA II 3º FISICO MATEMATICO - MATEMATICA III 3º SOCIAL ECONOMIA

MATEMATICA II: 3º FISICO MATEMÁTICA (Reformulación 2006)
MATEMATICA III: 3º SOCIAL ECONOMÍA (Reformulación 2006)
APLICACIONES DE LA PARÁBOLA: PROPIEDAD ÓPTICA:

Una propiedad geométrica simple de la parábola es la base de muchas aplicaciones importantes.
Si F es el Foco y P es un punto cualquiera de la parábola, la tangente en P forma ángulos iguales con FP y con GP que es paralela al eje de la parábola.
Un principio de física dice que cuando un rayo de luz choca contra una superficie reflectora, el ángulo de incidencia es igual al ángulo de reflexión.
Si la parábola gira en torno a su eje se forma un paraboloide de revolución con una superficie reflectora, de modo que todos los rayos que partan del Foco se reflejarán después de chocar con la superficie reflectora paralelos al eje de la parábola.

Esta propiedad de la parábola se usa en el diseño de faros buscadores en los que la fuente de luz se coloca en el foco. Recíprocamente, se usa en ciertos telescopios en los que los rayos paralelos provenientes de una estrella lejana que entran, son enfocados hacia un solo punto: el Foco.

Demostración de la propiedad óptica:
QP es la tangente en P y GP la paralela al eje de las ordenadas. Queremos demostrar que α = β.
Reducimos el problema a demostrar que el triángulo FQP es isósceles.
Hallaremos las coordenadas de Q y luego probaremos que FP = FQ.

El sonido y las ondas electromagnéticas obedecen las mismas leyes de la reflexión de la luz por lo que se usan micrófonos parabólicos para recoger y concentrar sonidos que provienen, por ejemplo, de una parte distante del estadio de fútbol.
Las antenas parabólicas utilizan la propiedad de reflexión de las ondas electromagnéticas para recibir o enviar señales a estaciones de radio, satélites de comunicación o galaxias remotas.

MATEMATICA II 2º CIENTIFICO REPARTIDO 5

Liceo de Nueva Palmira Dr. Medulio Pérez Fontana

MATEMATICA II 2° DC Reformulación 2006
REPARTIDO Nº 5 – NOTACIÓN CIENTÍFICA - Prof. Guillermo R. Osorio Salorio

1) Expresar en Notación científica los siguientes valores:

2) Completar las siguientes igualdades, de acuerdo al modelo:
3) Completar las igualdades siguientes de acuerdo al modelo:

4) 5) Efectuar las operaciones que se indican, a partir de las reglas para la división y multiplicación: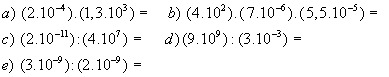
6) Efectuar las siguientes operaciones:

MATEMATICA II 2º CIENTIFICO REPARTIDO 4

Liceo de Nueva Palmira Dr. Medulio Pérez Fontana

MATEMATICA II PRACTICO 2° C - REPARTIDO Nº 4

CONJUNTOS NUMÉRICOS

1) Señala a qué conjuntos pertenecen los siguientes números Reales:

2) Ordenar en forma decreciente los siguientes números reales:

3) Representar los siguientes números racionales en forma de fracción:
4) Calcular sin hacer uso de la calculadora:

5) Simplificar las siguientes expresiones:

6) Hallar el valor de x:

7) Efectuar operaciones:

8) Calcular el resultado en forma de fracción:

9) Racionalizar los denominadores:

10) Simplificar las siguientes expresiones:

MATEMATICA II 3º FISICO MATEMATICO: APUNTES

LUGARES GEOMÉTRICOS EN EL PLANO
Traducido de: L. BRUN et L.TREVILLET
“EXERCISES DE GEOMETRIE”
Ediciones de La Casa del Estudiante – Junio de 1980

LUGARES GEOMÉTRICOS EN EL PLANO
I) Definición de un Lugar Geométrico
Supongamos un punto móvil que se desplaza en un plano a una distancia constante de un punto fijo O del mismo plano. Sabemos que ese punto recorrerá una circunferencia de centro O y radio la distancia constante ( R ). El conjunto de los puntos de la circunferencia y solamente ellos constituye el Lugar Geométrico de P. Un Lugar Geométrico es pues una figura cuyos puntos gozan de una cierta propiedad que no poseen los puntos que no pertenecen a la figura. Se puede concebir un aparato provisto de un lápiz que represente el punto móvil, traduce en forma continua el Lugar Geométrico de este punto. Un compás es un dispositivo simple de este tipo. También los diagramas obtenidos en los aparatos registradores son Lugares Geométricos.

II) Cinco Lugares Geométricos fundamentales:
1º) El lugar de los puntos situados a una distancia R de un punto fijo O es la circunferencia de centro O y radio R.

2º) El lugar de los puntos situados a una distancia dada d de una recta fija r es el conjunto de dos paralelas a r trazadas a la distancia d de esta recta.

3º) El lugar de los puntos equidistantes de dos puntos fijos A y B es la mediatriz del segmento AB.

4º) El lugar de los puntos equidistantes de dos semirrectas Ox y Oy es la bisectriz del ángulo xOy.

5º) El lugar de los puntos desde los cuales se ve un segmento de recta AB bajo un ángulo dado está formado por dos arcos de circunferencia que tienen AB por cuerda y se llaman arcos capaces del ángulo dado sobre el segmento AB. Estos dos arcos son simétricos con respecto a AB. Cada centro está para la mediatriz de AB y sobre la perpendicular en B a la recta que forma con AB un ángulo igual al dado. Si el ángulo es menor que un ángulo recto, cada arco capaz es mayor que una semicircunferencia. Si es recto, cada arco es una semicircunferencia. Si es mayor, cada arco es menor que una semicircunferencia.

III) Estudio de un Lugar Geométrico.
Búsqueda del lugar y demostración.
Es útil tratar de tener una idea de la naturaleza del lugar. Para ello, podemos construir varias posiciones. Puede suceder:
1º) Que las construcciones efectuadas den puntos alineados: tenemos la intuición de que el lugar es una recta y trataremos de demostrarlo.
2º) Que los puntos no estén alineados. Como por el momento, tratándose de lugares planos la única curva que hemos estudiado es la circunferencia, podemos tener la intuición de que se trata de una circunferencia ( o de un arco) y trataremos de demostrarlo.
Para establecer el lugar que acabamos de intuir, trataremos de ubicar el problema en uno de los logares del parágrafo II.

1er. ejemplo:
Sean A y B dos puntos fijos de una recta xy. Se traza una circunferencia variable C tangente en B a xy y desde A se traza la segunda tangente AM a la circunferencia. Lugar Geométrico de M.

Búsqueda del Lugar: Construimos tres posiciones particulares M1, M2 y M3 del punto M (fig. 1). Observamos que estos puntos no están alineados y parecen pertenecer a una circunferencia de centro A. Para demostrarlo bastará con probar que la distancia AM es constante. Este estudio preliminar debe ser hecho “en borrador” solo para guiarse. Para hacer la demostración haremos una nueva figura con la única posición de M (Fig. 2).
Demostración: Las longitudes AM y AB son iguales por ser tangentes desde un mismo punto exterior A a la circunferencia de centro O. Como A y B son fijos, la longitud AM es constante y el punto M se desplazará sobre la circunferencia de centro A y radio AB.
Recíproco: Habiendo ya demostrado que el punto M se halla sobre una figura fija, falta probar que un punto tomado sobre esta figura responde a las condiciones impuestas a M por el enunciado.
Haremos una nueva figura (fig.3) que tenga los elementos fijos de la hipótesis del problema y el lugar hallado en la primera parte.
Sea M un punto de la circunferencia de centro A y radio AB. Bastará demostrar que se puede construir una circunferencia tangente en M a AM y tangente en B a AB. Tracemos la perpendicular en M a AM y en B a AB. Estas rectas se cortan en O (siempre que M no pertenezca a la recta AB). Son tangentes a la circunferencia de centro A siendo perpendiculares respectivamente a los radios AM y AB en sus extremos. Estas dos tangentes OB y OM son iguales. Por tanto la circunferencia de centro O y radio OB pasará por M. Será tangente en B a AB y en M a AM, ya que estas rectas son perpendiculares a los radios OB y OM en sus extremos. M es entonces el punto de contacto de una tangente trazada desde A a una circunferencia tangente en B a AB.
La conclusión de este estudio es que el lugar de M es la circunferencia de centro A y de radio AB, exceptuando los puntos B y diametralmente opuestos para los que no puede trazarse la circunferencia del enunciado. El recíproco muestra si toda la figura hallada constituye el lugar buscado, o si el lugar está solo formado por parte de la figura (como en el caso anterior en que debimos excluir dos puntos). En este último caso, será determinar los límites del lugar.
Se puede considerar un problema de lugar geométrico como el estudio de una figura que se deforma manteniendo ciertos elementos fijos. La figura queda completamente determinada cuando se elige la posición de un cierto punto o de una cierta recta que llamaremos variable principal. Este elemento se desplaza entre dos posiciones límites fijadas en el enunciado. (Estas posiciones pueden estar confundidas, por ejemplo si un punto, elemento variable principal, describe una circunferencia).
A cada una de estas posiciones del elemento variable principal corresponde una posición particular del punto cuyo lugar se busca. Estas posiciones particulares son los límites del lugar. La búsqueda completa de los límites de un lugar puede sustituir al recíproco.
Veamos un ejemplo:

2º ejemplo): Sea P un punto fijo exterior a una circunferencia de centro O. Se traza una secante PAB a la circunferencia. Lugar Geométrico del punto medio de la cuerda AB.

Búsqueda del lugar: (en borrador). Construimos tres posiciones de la secante PAB. Los puntos medios de las cuerdas son respectivamente M1, M2 y M3 que no están alineados. Parecen pertenecer a una circunferencia de diámetro PO (O es un punto del lugar ya que PO corta a la circunferencia, según un diámetro de punto medio O).
Demostración: Siendo M el punto medio de la cuerda AB, la recta OM que une ese punto al centro es perpendicular a AB. Por tanto el ángulo OMP es recto; es inscriptible en una semicircunferencia de diámetro OP, M pertenece entonces a la circunferencia de centro C, medio de OP.
Recíproco: Sea M un punto de la circunferencia C de diámetro OP. Trazamos PM que corta a la circunferencia en A y B. El ángulo OMP está inscrito en una semicircunferencia; es recto. por tanto OM es perpendicular a la cuerda y pasa por el punto medio de AB, M es el punto medio de AB.

Para que este razonamiento sea válido se necesita que PM encuentre a la circunferencia de centro O y por tanto que M esté sobre la parte de la circunferencia interior al círculo de centro O, es decir sobre el arco TOT’.
Limitación del lugar: Podríamos haber hallado los límites del lugar por el razonamiento siguiente, que puede sustituir al recíproco. En este problema, el elemento variable principal es la recta PAB. Gira alrededor de P y debe encontrar a la circunferencia de centro O. Sus posiciones límites son las tangentes PT y PT’ a la circunferencia de centro O. Para la posición PT los puntos A y B están confundidos en T, por tanto el punto medio M de AB es también T. para la posición PT’, M está en T’. El lugar es el arco TOT’ de la circunferencia de diámetro OP, interior al círculo de centro O.

Utilización de las posiciones particulares:
La posición notable de la secante PAB pasando por O nos ha mostrado que O es un punto del lugar. Se puede a veces, considerando posiciones particulares del elemento variable, deducir posiciones (sin construcciones nuevas) de puntos del lugar. Por otra parte, estos puntos son en general los límites del lugar.
Algunas veces el punto móvil puede halarse sobre una línea fija ya trazada. Es suficiente en este caso construir la figura para tener una idea del lugar. La demostración consiste en justificar esta posición notable. Veamos otro ejemplo:

3er. ejemplo: Sea un punto M variable exterior a una circunferencia de centro O. Se trazan las tangentes MA y MB. Lugar del incentro del triángulo MAB.

Búsqueda del lugar (en borrador): Las bisectrices de los ángulos MAB y MBA parecen cortarse sobre la circunferencia de centro O.

Demostración: La bisectriz del ángulo A pasa por el punto medio del arco AB. Los dos ángulos inscritos A1 y A2 iguales deben interceptar arcos iguales. La bisectriz del ángulo B también pasa por el punto medio del arco AB. El incentro pertenece a la circunferencia de centro O.

Recíproco: Sea I un punto de la circunferencia de centro O. Tracemos una cuerda AB perpendicular a OI y las tangentes en A y B se cortan en M. El radio OI perpendicular a la cuerda AB pasa por el punto medio del arco AB y los arcos AI e IB son iguales. El ángulo A1 inscrito es igual a la mitad del ángulo BOI y el A2 semiinscrito igual a la mitad del IOA. Entonces los ángulos A1 y A2 son iguales, AI es la bisectriz del ángulo MAB.
Análogamente, BI es bisectriz del ángulo MBA, I es entonces el incentro del triángulo.
El Lugar de I es la circunferencia de centro O entera..

También el punto móvil puede estar sobre una línea fija no trazada en la figura y no incluida en los cinco lugares del parágrafo II. En este caso nos encontramos en general en presencia de una recta. Se prueba que es fija mostrando que pasa por un punto fijo y forma un ángulo constante con una dirección fija.

4to. Ejemplo: Sea M un punto variable del lado AB de un triángulo ABC. Se toma sobre la prolongación CX de AC una longitud CN = BM. Lugar del vértice P del paralelogramo BMNP.

Búsqueda del lugar: Sea P el cuarto vértice del paralelogramo BMNP. Si M está en B, N está en C y el paralelogramo se reduce al segmento BC, por tanto P está en C. Si M está en A, el paralelogramo es BAN’P’. Los tres puntos del lugar C, P y P’ parecen alineados.

Demostración: Unimos C con P. Los lados opuestos BM y PN del paralelogramo son iguales, de donde PN = CN. El triángulo NCP es isósceles y el ángulo C1 es la mitad del ángulo externo N1. Pero NP y AB son paralelas. Los ángulos correspondientes N1 y A son iguales, por tanto el ángulo C1 es igual a la mitad del ángulo A, es un ángulo constante y la dirección CP es fija.

Recíproco: Sea P un punto de la recta CY que forma en C con CX un ángulo XCY igual al ángulo A/2. La paralela trazada por P a BA corta a CX en N y la paralela a PB trazada por N corta a AB en M.
En el triángulo NCP el ángulo externo N1 = C1 + P1 = N1 = A por correspondientes y C1 = A/2, de donde el ángulo P1 = A/2 = C . El triángulo NCP es isósceles y NP = CN . Los lados opuestos BM y PN del paralelogramo BMNP son iguales CN = BM y P es un punto del lugar.

Limitación: Los límites son C y P’

Construcción del lugar: Se traza la bisectriz del ángulo A y por C la paralela. por B se traza la paralela a AC para determinar P’

En resumen: Frente al problema de “Hallar el lugar geométrico de un punto P sujeto a ciertas condiciones“, lo resolvemos de la siguiente manera:
Buscamos una figura F sobre la cual se hallan todos los puntos P, y, luego, demostramos que todo punto de F (o parte de ella) cumple las condiciones exigidas.

El Lugar de una recta (o varias) si el punto móvil:
a) está a una distancia constante de una recta fija, el Lugar son las dos paralelas a la recta fija.
b) equidista de dos puntos fijos A y B, el Lugar es la mediatriz del segmento AB.
c) equidista de dos rectas fijas, el Lugar es la bisectriz de los ángulos formados por las rectas.
d) se halla en una recta que pasa por un punto fijo y forma un ángulo constante con una dirección fija.
e) se halla en una recta notable de la figura.

El Lugar en una circunferencia ( o parte) si el punto móvil:
a) está a una distancia constante R de un punto fijo O, el Lugar es una circunferencia de centro O y radio R.
b) es vértice de un ángulo constante cuyos lados pasan cada uno por un punto fijo, el Lugar es un arco capaz.
c) pertenece a una circunferencia fija de la figura.

A menudo, en los problemas del Lugar Geométrico hay que demostrar que un segmento o un ángulo son constantes.
A) se puede demostrar que son iguales a un segmento o un ángulo de la figura.
B) se los puede calcular en función de otros elementos de la figura y probar que el valor obtenido es constante,.

EJERCICIOS:
I) El punto móvil se encuentra a una distancia constante de un punto fijo

1) Lugar geométrico de los centros de las circunferencias de radio R que pasan por un punto fijo A.

2) Lugar Geométrico de los centros de las circunferencias tangentes a dos circunferencias concéntricas dadas.

3) Lugar Geométrico de los puntos desde los cuales se puede trazar dos tangentes a una circunferencia que formen entre ellas un ángulo dado.

4) Sea un ángulo recto XOY fijo, y un segmento AB que se desplaza de modo que A pertenece siempre a OX y B a OY, siendo el segmento AB de longitud constante. Hallar el Lugar Geométrico del punto medio M de AB. Se trazan las perpendiculares en A a OX y en B a OY. Lugar Geométrico de la intersección de estas dos perpendiculares.

II) El punto móvil se halla a una distancia constante de una recta fija.

5) Una circunferencia de radio constante rueda sobre una recta XY. Lugar Geométrico de su centro.

6) Sea un paralelogramo ABCD cuyo lado AB es fijo y su altura CH constante. Lugar geométrico del punto de corte de las diagonales.

III) El punto móvil equidista de dos puntos fijos

7) Lugar geométrico de los vértices B y D de un rombo ABCD cuyos vértices A y C son fijos.
8) Lugar geométrico de las circunferencias tangentes a dos circunferencias iguales.

9) Sean tres puntos A, B y C alineados. Se consideran dos circunferencias iguales variables, una que pasa por A y B y la otra que pasa por B y C. Lugar Geométrico del segundo punto de intersección de las circunferencias.

IV) El punto móvil equidista de dos rectas fijas

10) Lugar geométrico de los centros de la circunferencia tangente a dos rectas paralelas.

11) Sea un cuadrado ABCD. Se toma sobre la prolongación del lado BC un punto M. La perpendicular en A a AM corta la prolongación de CD en P. Se construye el paralelogramo AMNP. Lugar Geométrico del vértice N.

12) Sea una circunferencia de centro O y dos diámetros X’OX e Y’OY perpendiculares. Un ángulo recto AOB gira alrededor de O. Sus lados cortan la circunferencia respectivamente en A y B. Por A se traza una paralela a X’OX y por una a Y’OY. Lugar Geométrico del punto P de intersección de estas dos rectas.

V) El punto móvil pertenece a un arco capaz.

13) En un triángulo ABC, el lado BC es fijo y el punto A es cualquiera. Lugar Geométrico de los pies de las alturas trazadas desde B y C.

14) En un triángulo ABC el lado BC es fijo y el punto A es cualquiera tal que el ángulo A es constante. Lugar Geométrico del centro de la circunferencia inscrita en el triángulo (incentro).

15) En el triángulo ABC el lado BC es fijo, el ángulo A es constante. Lugar del ortocentro del triángulo ABC.

VI) El punto móvil pertenece a una línea fija de la figura

16) Sea A un punto fijo de una recta XY. Se consideran dos circunferencias variables cuyos centros pertenecen a XY y que son tangentes exteriormente en A. Se traza una tangente común exterior TT’. Lugar Geométrico del punto medio de TT’.

17) Sea M un punto variable de un segmento de recta AB. Se construye en una de los semiplanos determinados por la recta AB los cuadrados AMCD y BMEF. Lugar Geométrico de los centros I y J de estos cuadrados. Lugar Geométrico del punto medio de IJ.

VII) El punto móvil se encuentra sobre una recta que pasa por un punto fijo y forma un ángulo constante con una dirección fija.

18) Sea un ángulo XOY de 60º. Sobre OX y OY se toman dos segmentos iguales OA y OB. Se traza BA y se prolonga en una longitud AK, BA. Lugar Geométrico del punto K cuando A describe OX. Lugar Geométrico del circuncentro del triángulo OAK.

VIII) Los lugares siguientes se reducen a los casos precedentes

19) Lugar Geométrico del vértice A de u triángulo ABC cuyo lado BC es fijo y la altura AH es constante.

20) Lugar Geométrico de los puntos medios de las cuerdas de longitud d trazadas en una circunferencia de radio R.

21) Sea una recta fija XY y un punto fijo A exterior a la recta. Sea B un punto variable de XY. Se prolonga AB es una longitud BP=AB. Lugar Geométrico de P.

22) Sobre los lados AB y AC de un triángulo isósceles ABC se toma AM = AN. Lugar Geométrico del punto de intersección de las rectas CM y BN.

23) Sea un triángulo equilátero ABC cuyo vértice A es fijo. El lado BC pasa por un punto fijo M. Lugar Geométrico de los vértices B y C.

24) En un triángulo ABC el lado BC es fijo y el ángulo A es constante. Lugar Geométrico del centro de la circunferencia exinscrita en el ángulo B del triángulo. Idem para la circunferencia exinscrita en el ángulo C.

25) Sea AC una cuerda variable de una semicircunferencia de diámetro AB y sea AX la tangente a esta semicircunferencia. La bisectriz del ángulo CAX corta BC en un punto M. Lugar Geométrico de M.

26) En un triángulo ABC el lado BC es fijo, el vértice A cualquiera. Lugar geométrico de las proyecciones de los vértices B y C sobre la mediana trazada desde A.

MATEMATICA II 3º FISICO MATEMATICO ACTIVIDAD 8

MATEMATICA II: 3º FISICO MATEMÁTICA (Reformulación 2006)
ACTIVIDAD No. 8: GEOMETRÍA DEL ESPACIO: SECCIONES PLANAS – AREAS Y VOLÚMENES

1) Se considera un Cubo ABCDEFGH cuya arista es de medida dada “a” y los planos α = (A,H,F) y β =(A,E,C).
a) Construir en verdadera magnitud la sección plana del cubo con α .
b) Indicar que tipo de poliedro es el AHFC y construir un desarrollo del mismo.
c) Construye en verdadera magnitud la sección plana del poliedro AHFC con el plano β .

2) La base de una pirámide es un rectángulo ABCD con BC = x y AB = 2x . El vértice V está sobre la perpendicular por el centro del rectángulo tal que la altura de la pirámide es x.
a) Calcular la superficie total y el Volumen de la pirámide.
b) Construir el desarrollo.
c) Construir la intersección de la pirámide con el plano que contiene el lado CD y es perpendicular al plano (A,B,V). Calcular el área de dicha sección (para la construcción tomar x= 2 cm)

3) Se considera un Cubo ABCDEFGH de arista x. Sean P y Q los puntos medios de las aristas AE y AB respectivamente, y M y N que pertenecen a las aristas CD y DH tales que MD = ND = x/3
a) Construir para x = 4 cm el cuadrilátero PQMN.
b) Calcular el área en función de x.
c) Calcular en función de x el área total y el Volumen del poliedro APQDNM.

MATEMATICA IV 3º MATEMATICA y DISEÑO: ACTIVIDAD 5

MATEMATICA IV: 3º MATEMÁTICA Y DISEÑO (Reformulación 2006)
ACTIVIDAD No. 5: GEOMETRIA DESCRIPTIVA: REPRESENTACIÓN DE RECTAS

1) Una recta es paralela a LT, encontrar su distancia a LT

2) Dar las proyecciones de una recta que pasando por un punto P de cota 5 y alejamiento 2, es paralela al PV y forma un ángulo de 30º con el PH

3) Hallar la intersección de una horizontal y una vertical con el primer bisector

4) Trazar por el punto P (4 ; -2) una recta paralela a una recta de perfil dada por los puntos
M (-1 ; -5) y N (-4 ; 1)

5) Trazar en el primer diedro, por el punto A (3 ; 1), una recta que forme con el PH un ángulo de 30º y con el PV un ángulo de 45º

6) a) Representar una pirámide VABCD cuya base ABCD es un rectángulo, sabiendo además:
• A (3 , 2 , 0) , C ( 7 , 4) , V (5,....,0).
• AB // PV, B tiene cota 4, AB = 5cm, AV = 5cm (B a la derecha de A).
b) Justificar la determinación de B, C y V.

7) a) Representar un tetraedro regular ABCD de 5cm de arista, sabiendo:
• M (6,6) y N son puntos medios de AB y CD respectivamente
• el plano (CDM) está contenido en el 1er. Bisector
• CD // LT (C y D con la menor cota posible)
b) Justificar la determinación de los vértices del tetraedro.

8) a) Dados A(5,3,0), B(1,2,2), C(5,2,5), D(3,-3,5), E(-2,2,6), hallar la “verdadera magnitud” de los segmentos: AB, AC, ,BC, ,CD y DE
b) Dados : Una recta r cualquiera y los puntos A perteneciente a “r” y B no perteneciente a “r”, representar un triángulo ABC isósceles con base BC , con AC incluida en r .
c) Representar P(2,3) y Q(5,4) / PQ = 8cm.

9) Representar un cubo ABCDEFGH sabiendo que :
a) arista= 4cm, A(1,2), AB es frontal, cot(B)=3cm (B a la derecha de A), cot(C) = 4cm (con el mayor alejamiento posible). E con la mayor cota posible.
b) arista= 4cm, A(2,3), AB de perfil, alej(B)=3cm, alej(G)=6cm
c) A(4,5), F(1,3), AF = 5cm. alej(H)=4cm, H y E con la menor cota posible.

10) Representar un octaedro regular ABCDEF sabiendo que :
a) O (7,6), (O centro del octaedro), arista=4cm, B(5,5), alej(C)=6,5cm
b) AD es horizontal, arista=4cm, A(3,4), alej (D)=5cm (D a la derecha de A), A'F' = 3cm.
O con la mayor cota posible.

MATEMATICA III 3º SOCIAL ECONOMIA - ACTIVIDAD 5

LICEO DE NUEVA PALMIRA “Dr. Medulio Pérez Fontana”
MATEMÁTICA III 3º SOCIAL ECONOMIA - Prof. Guillermo R. Osorio Salorio
ACTIVIDAD Nº 5 –PROGRAMACIÓN LINEAL – TRABAJANDO CON GEOGEBRA

1) Un agricultor posee 22 hectáreas de tierras de labor. Debe sembrar Cebada y Papas.
De papas, por razones de cupo, le está permitido plantar hasta 10 hectáreas. Los costos de roturación, simiente y abono son de u$s 700 por hectárea para la Cebada y de u$s 2100 por hectárea para las papas.
Para cubrir esta inversión inicial, el productor dispone de u$s 25200.
Tras la recolección y la venta del producto, cada hectárea le reporta: u$s 2200 la Cebada y u$s 850 las papas. ¿Cuántas hectáreas de cada cultivo debe sembrar para hacer máximo el beneficio o ganancia?

2) Una compañía posee dos minas. La mina A produce diariamente dos toneladas de carbón de alta calidad, cuatro toneladas de carbón de calidad media y ocho toneladas de carbón de baja calidad.
La mina B produce cuatro toneladas de cada clase de carbón.
La compañía necesita 140 toneladas de carbón de alta calidad, 260 toneladas de calidad media y 300 toneladas de baja calidad. Los gastos diarios de la mina A ascienden a u$s 300 y los de la mina B a u$s 400. ¿Cuántos días hay que trabajar en cada mina para que el costo sea mínimo?

3) Con 80 Kg de acero y 120 Kg de aluminio se quieren fabricar bicicletas de Montaña y de Paseo que se venderán a u$s 200 y u$s 150 respectivamente.
Para una bicicleta de montaña son necesarios 1 Kg de acero y 2 Kg de aluminio y para unba de paseo 2 Kg de cada uno de los metales. ¿Cuántas bicicletas de montaña y de paseo se deben fabricar para obtener el beneficio máximo? ¿A cuánto asciende éste?

4) En una granja se preparan dos clases de alimentos para el ganado: P y Q, mezclando dos productos A y B. Una bolsa de P contiene 8 Kg de A y 2 Kg de B, y una bolsa de Q contiene 10 Kg de A y 5 Kg de B. Cada bolsa de P se vende a $300 y cada bolsa de Q se vende a $800. Si en la granja hay almacenados 80 Kg de A y 25 Kg de B ¿Cuántas bolsas de cada tipo de alimento para ganado deben prepararse para obtener los máximos ingresos?

5) Una campaña para promocionar una marca de productos lácteos se basa en el reparto gratuito de yogures con sabor a Frutilla o Durazno. Se decide repartir al menos 30000 yogures en el departamento de Colonia. Cada yogur de Frutilla necesita para su elaboración 0,5 gramos de un producto de fermentación y cada yogur de Durazno necesita 0,2 gramos de este mismo producto. Se dispone de 9 Kg de este producto para fermentación. El costo de producción de un yogur de Frutilla es de $3 y $2 para uno de Durazno.
¿Cuántos yogures de cada clase se deberán repartir para que el costo sea mínimo?

6) Disponemos de u$s 210.000 para invertir en bolsa. Nos recomiendan dos tipos de acciones. Las del tipo A, que rinden el 10% y las del tipo B, que rinden el 8%. Decidimos invertir un máximo de u$s130.000 en las del tipo A y como mínimo u$s 60.000 en las del tipo B. Además queremos que la inversión en las del tipo A sea menor que el doble de la inversión en B. ¿Cuál tiene que ser la distribución de la inversión para obtener el máximo interés anual?

7) Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos. Por necesidades de mercado, es necesario que haya mayor o igual número de mecánicos que de electricistas y que el número de mecánicos no supere al doble que el de electricistas. En total hay disponibles 30 electricistas y 20 mecánicos. El beneficio de la empresa por jornada es de $ 2500 por electricista y $ 2000 por mecánico. ¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo beneficio y cual es este?

MATEMATICA III 3º SOCIAL ECONOMIA - INTRODUCCIÓN A LA PROGRAMACIÓN LINEAL

Introducción a la Programación Lineal:
Se buscan soluciones

En el mundo en el que vivimos cada vez más se hace necesario desarrollar técnicas que nos permitan gestionar el funcionamiento de una compañía aérea asegurando eficacia y rentabilidad, buscarlos mejores canales de distribución para los productos de una multinacional, encontrar la composición ideal para un alimento para el ganado, planificar la producción de una fábrica o decidir medidas para el ahorro energético de grandes empresas.

Aún cuando la programación lineal surgió especialmente para dar respuesta a cuestiones de carácter logísitco y militar, es en la industria y en la economía donde posteriormente ha encontrado sus aplicaciones más interesantes.
En los problemas prácticos con los que nos encontramos en el mundo actual intervienen multitud de factores (materia prima, mano de obra, transporte, recursos disponibles, niveles económicos, tiempo, etc.) sujetos a múltiples restricciones, con los que se desea obtener unos beneficios máximos o unos costos mínimos.

Detrás de todas estas situaciones se esconde un problema de optimización. Encontrar una solución óptima significa hallar la mejor solución a un problema sujeto a restricciones. En el caso de la multinacional, se trataría de minimizar el gasto derivado de la distribución de los productos y las restricciones serían por ejemplo el tiempo de entrega, cubrir una zona determinada, etc.
Si hablamos del diseño de la producción de la fábrica, se trataría de maximizar las ganancias; las restricciones serían la materia prima disponible, las exigencias del mercado, etc. En todos ellos, las restricciones se pueden traducir en inecuaciones lineales y lo que se va a minimizar o maximizar en una función lineal.

La programación lineal es un sistema matemático de resolución de problemas muy empleado por ingenieros, hombres de empresa, economistas, etc., que aplican la matemática para resolver problemas concretos. De una manera intuitiva, todos nosotros empleamos la programación lineal para resolver problemas, aunque no vendría nada mal aprender a hacerlo de manera sistemática como hacen los profesionales antes aludidos.

Un problema de programación lineal para dos variables consiste en:
1) Optimizar( maximizar i minimizar) una función lineal a la que llamaremos Función Objetivo.
2) Esa Función Objetivo está sujeta a restricciones, dadas mediante inecuaciones lineales.

Cada desigualdad anterior determina un semiplano. El conjunto de los puntos que cumplen todas las desigualdades determinan un recinto, acotado o no, que llamaremos Región Factible.
Se llama solución óptima a una solución factible que optimice la Función Objetivo.
El teorema fundamental de la programación lineal dice que la solución óptima se encuentra siempre en la frontera de la región factible.

Veamos dos ejemplos:
Ejemplo 1:Problema de máximos.
En una granja se preparan dos clases de alimentos para el ganado: P y Q, mezclando dos productos A y B. Una bolsa de P contiene 8 Kg de A y 2 Kg de B, y una bolsa de Q contiene 10 Kg de A y 5 Kg de B. Cada bolsa de P se vende a $300 y cada bolsa de Q se vende a $800. Si en la granja hay almacenados 80 Kg de A y 25 Kg de B ¿Cuántas bolsas de cada tipo de alimento para ganado deben prepararse para obtener los máximos ingresos?

Ejemplo 2: Problema de mínimos
Una campaña para promocionar una marca de productos lácteos se basa en el reparto gratuito de yogures con sabor a Frutilla o Durazno. Se decide repartir al menos 30000 yogures en el departamento de Colonia.
Cada yogur de Frutilla necesita para su elaboración 0,5 gramos de un producto de fermentación y cada yogur de Durazno necesita 0,2 gramos de este mismo producto. Se dispone de 9 Kg. De este producto para fermentación.
El costo de producción de un yogur de Frutilla es de$3 y $2 para uno de Durazno.

MATEMATICA II 3º FISICO MATEMATICO ACTIVIDAD 7

MATEMATICA II: 3º FISICO MATEMÁTICA (Reformulación 2006)
ACTIVIDAD No. 7: GEOMETRÍA DEL ESPACIO – Prof. Guillermo R. Osorio Salorio
SECCIONES PLANAS: TOMOGRAFÍAS

Una de las técnicas más modernas empleadas en medicina para obtener una radiografía del interior de un organismo se llama Tomografía de Resonancia Magnética Nuclear y se utiliza desde el año 1982. El procedimiento en el que está basado consiste en obtener imágenes del interior del cuerpo mediante capas paralelas sucesivas. Cada una de estas capas reproduce una imagen del organismo como si se hubiese realizado en él un corte. En cierta medida, cuando cortamos un poliedro por planos paralelos, la serie de cortes es una tomografía del cuerpo que podemos presentarla en una serie de radiografías.

A continuación te presentamos una serie de tomografías de cuerpos diferentes ¿Puedes hacer un dibujo aproximado de cada cuerpo?

1)

2)
3)
4)
5)
6) ¿Qué cuerpo sólido situado en cualquier posición produce siempre figuras de la misma forma aunque de distinto tamaño al cortarlo por planos paralelos, esto es, al hacerle una tomografía?

MATEMATICA IV 3º MATEMATICA y DISEÑO: ACTIVIDAD 4

MATEMATICA IV: 3º MATEMÁTICA Y DISEÑO (Reformulación 2006)
ACTIVIDAD No. 4: GEOMETRIA DESCRIPTIVA: REPRESENTACIÓN DE PUNTOS
Prof. Guillermo R. Osorio Salorio

1) Representar en un depurado los siguientes puntos: A(4 , 3 , 0) , B(3 , 5 , 1) , C(4 , -1 , 2) ,

D(2 , - 4 , 3) , E(-1 , -3 , 4) , F( -3 , -2 , 5) , G(-4 , 1 , 6) , H(-2 , 5 , 7) , I(2 , -2 , 8) , J(1 , 1 , 9)
(La tercer coordenada es la distancia de las líneas de referencia de los puntos respecto de la línea de referencia del punto A; hacia la derecha de A son positivas y hacia la izquierda de A son negativas).
a) Indicar en qué diedros se encuentran.
b) Indicar su ubicación son respecto a los planos de proyección y los bisectores.

2) Dado el punto A(3 , 4) hallar los puntos simétricos de A con respecto a los planos de proyección y a LT.

3) Representar A y B que son los extremos de un segmento de 6u paralelo a PH sabiendo que A tiene cota 3u y pertenece al 1er. Bisector.

4) Dado un punto A situado en PH, hallar otro punto de dicho plano que diste 5u de A y 2u de LT.

5) Dado un punto A(-1 , -4) del tercer diedro, hallar otro punto de su mismo diedro de igual alejamiento que A y que diste 3u del PH y 4u del punto dado.

6) Dados A(4 , 3) y B’ perteneciente a LT, representar un triángulo equilátero ABC de 7u de lado con el punto C en el PH anterior y AoB’ = 3u

7) Representar una pirámide VABC con : A(1 , 2 , 0) , B(4 , 4 , 1) , V(2 , 1 , 2) , C(2 , 2 , 4).

8) Representar un cubo ABCDEFGH de 6u de arista con (ABC) en el PH, A(0 , 5) , B(0 , 7)
C con el mayor alejamiento posible y E con la mayor cota.

9) Representar un tetraedro regular ABCD de 6u de arista con una cara ABC en un plano de perfil. A(2 , 3) , B tiene cota 3u (con el mayor alejamiento). D lo más a la izquierda posible.

10) Representar un octaedro regular de 5u de arista con (ABC) en el 1er Bisector , AB//LT (A y B con 5u de cota ). C y D con la mayor cota posible.

MATEMATICA III 3º SOCIAL ECONOMIA - ACTIVIDAD 4

LICEO DE NUEVA PALMIRA “Dr. Medulio Pérez Fontana”
MATEMÁTICA III 3º SOCIAL ECONOMIA
ACTIVIDAD Nº 4 –TRABAJANDO EN EL PLANO - Prof. Guillermo Osorio Salorio

1) Representar con Rojo el conjunto A de los puntos del plano cuya abcisa es estrictamente positiva. Completar: A= {(x;y) / ………………}

2) Representar con Rojo el conjunto B de los puntos del plano cuya ordenada es negativa o nula. Completar: B= {(x;y) / ……………….}

3) Representar con Rojo el conjunto C de los puntos del plano cuya ordenada es igual a la abcisa. Completar: C= {(x;y) /……………….}

4) Representar con Rojo el conjunto D de los puntos del plano cuya ordenada es estrictamente inferior a la abcisa. Completar: D= {(x;y) /………………}

5) Representar con Rojo el conjunto E de los puntos del plano cuya ordenada es el doble de la abcisa. Completar: E= {(x;y) / ………………….}

6) Representar con Rojo el conjunto F de los puntos del plano cuya ordenada es opuesta a la abcisa. Completar: F= {(x;y) /………………….}

7) Representar con Rojo el conjunto G de los puntos del plano cuya ordenada es la mitad de la abcisa. Completar: G= {(x;y) / ……………….}

8) Representar con Rojo el conjunto H de los puntos del plano cuya ordenada es igual a la opuesta del doble de la abcisa. Completar: H = {(x;y) / ………………}

9) Representar con Rojo el conjunto I de los puntos del plano cuya ordenada es el triple de la abcisa menos dos unidades. Completar: I= {(x;y) / ……………….}

10) Representar los siguientes semiplanos cuyas ecuaciones son:

11) Representar en el plano las soluciones de los siguientes sistemas de inecuaciones. Hallar las coordenadas de los vértices de las regiones poligonales resultantes.

MATEMATICA IV 3º MATEMATICA y DISEÑO: GEOMETRIA DESCRIPTIVA PROYECCIONES DE RECTAS DEL PLANO

Geometría-Descriptiva.-Rectas del Plano

View more presentations or Upload your own.

MATEMATICA IV 3º MATEMATICA y DISEÑO: GEOMETRIA DESCRIPTIVA PROYECCIONES DEL PLANO

Geometría-Descriptiva.-Planos

View more presentations or Upload your own.

MATEMATICA IV 3º MATEMATICA y DISEÑO: GEOMETRIA DESCRIPTIVA PROYECCIONES DE LA RECTA

Geometría-Descriptiva.-Rectas

View more presentations or Upload your own.

MATEMATICA IV 3º MATEMATICA y DISEÑO: GEOMETRIA DESCRIPTIVA PROYECCIONES DEL PUNTO

Geometría-Descriptiva.-Puntos

View more presentations or Upload your own.

MATEMATICA II 3º FISICO MATEMATICO ACTIVIDAD 5

Matematica II 3º Fisico Matematica Actividad 5

View more Microsoft Word documents from guest1c433c.

MATEMATICA II 3º FISICO MATEMATICO ACTIVIDAD 5

Matematica II 3º Fisico Matematica Actividad 5

View more Microsoft Word documents from guest1c433c.

MATEMATICA III 3º SOCIAL ECONOMIA - ACTIVIDAD 3

LICEO DE NUEVA PALMIRA “Dr. Medulio Pérez Fontana”
MATEMÁTICA III 3º SOCIAL ECONOMIA - ACTIVIDAD Nº 3
MATRICES Y DETERMINANTES - Prof. Guillermo Osorio Salorio

1) Justifique sin calcularlos porqué los siguientes determinantes son nulos:

2) extraer factores de:
3) Sabiendo que:

4) Calcular los siguientes determinantes:

5) Calcular de dos formas: Por Sarrus y desarrollando por una fila o columna:

6) Calcular los siguientes determinantes:

7) Calcular sabiendo que un determinante no varía si a cada fila le restamos la anterior:

8) Los siguientes determinantes se denominan de Van Der Monde. Calcularlos. (Indicación: Resta a cada fila la anterior multiplicada por a)

9) Dado determinar sin desarrollar que las raíces del polinomio son; 4; 8 y -12

10) Calcular si existen las inversas de las siguientes matrices:

11) A, B y X son matrices cuadradas. A es inversible.
a) Despejar X en las ecuaciones: i) XA = B ; ii) AX = B
b) Calcular X en los casos anteriores si:
12) Calcular la inversa para los valores de los parámetros que hagan inversible las matrices:

13) Utiliza la regla de Cramer y resuelve los siguientes sistemas:

14) Discutir los siguientes sistemas según el parámetro m: