MATEMATICA II 3º FISICO MATEMATICO ACTIVIDAD 1

LICEO DE NUEVA PALMIRA “Dr. Medulio Pérez Fontana”
MATEMÁTICA II - 3º FISICO MATEMÁTICAS ACTIVIDAD Nº 1

CRITERIOS DE IGUALDAD DE TRIÁNGULOS: Para investigar la igualdad de dos triángulos, es suficiente con verificar la igualdad de tres de sus elementos, debiendo verificarse por lo menos, una entre lados.

1er. Criterio: Dos triángulos son iguales si tienen respectivamente iguales dos lados y el ángulo comprendido (LAL)
2do. Criterio: Dos triángulos son iguales si tienen respectivamente iguales un lado y los dos ángulos adyacentes (ALA)
3er. Criterio: Dos triángulos son iguales si tienen respectivamente iguales sus tres lados (LLL)
4to. Criterio: Dos triángulos son iguales si tienen respectivamente iguales dos lados y el ángulo opuesto al mayor de ellos.

1) Sabiendo que , investigar si los segmentos CE y BD son iguales.
2) a) El triángulo ABC es equilátero, los segmentos AP, BQ, CR son iguales. Justificar que PQR es un triángulo equilátero.
b) ABCD es un cuadrado, los segmentos AP, BQ, CR y DS son iguales. Justificar que PQRS es un cuadrado.
3) M es punto interior a un triángulo ABC. Construir los puntos I, K, y L de tal modo que los cuadriláteros IAMB, AMCK y MCLB sean paralelogramos. Demostrar que los segmentos AL, BK y CI se cortan en su punto medio.

4) a) Demostrar que los puntos medios de los lados de un triángulo y uno de sus vértices, son los vértices de un paralelogramo.
b) ¿Qué relación hay entre las áreas del triángulo y del paralelogramo?
c) ¿Qué condición debe cumplir el triángulo para que el paralelogramo sea 1°) Rombo, 2°) Rectángulo, 3°) cuadrado.

5) Decir en cada caso si las siguientes proposiciones son verdaderas o falsas. Justificar las respuestas.
a) Si un cuadrilátero tiene un par de ángulos opuestos iguales es un paralelogramo.
b) Si un cuadrilátero tiene las diagonales iguales es un paralelogramo.
c) En todo paralelogramo los lados opuestos son iguales.
d) Si un cuadrilátero tiene las diagonales perpendiculares es un rombo.
e) Si un paralelogramo tiene las diagonales iguales es un rectángulo.

6) Construir utilizando solamente regla y compás los cuadriláteros ABCD.
a) ABCD es un paralelogramo, la diagonal
b) ABCD es un rectángulo, la diagonal , siendo O el centro del rectángulo.
c) ABCD es un rombo, el lado

7) El segmento AB es una cuerda de una Circunferencia C. Por A se traza la tangente t y se toma en ella un punto P tal que . D y B son los puntos de intersección de BP con C . Demostrar que el triángulo PDA es isósceles.

8) Se considera un rectángulo MNPQ antihorario inscripto en una circunferencia .La perpendicular a la recta MP por Q corta a C(O;r) en T y Q
a) Demostrar que el triángulo MOQ es equilátero.
b) Calcular la medida del ángulo TSN.

9) a) Calcular la diagonal de un cuadrado en función de su lado.
b) Calcular la diagonal de un cubo en función de su arista.
c) Calcular la altura de un triángulo equilátero en función de su lado.

10) a) MNP es un triángulo tal que ¿Es MNP un triángulo rectángulo?.
b) ABC es un triángulo tal que , siendo H el pie de la altura trazada desde A.¿El triángulo ABC, es rectángulo?

11) t y t’ son las tangentes a la circunferencia C(O;r) en los puntos T y T’;
a) Demostrar que
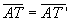
b) Indicar ángulos iguales determinados por los puntos T, T’, O y A

12) a) Demostrar que:
i) Todo ángulo recto inscripto en una circunferencia abarca un diámetro.
ii) Todo ángulo inscripto en una circunferencia que abarca un diámetro es un ángulo recto.
iii) Todo triángulo rectángulo está inscripto en una circunferencia de diámetro la hipotenusa.
b) ABC es un triángulo rectángulo en A. Probar que

13) Sabiendo que la medida de , calcular las medidas de los segmentos EO, AE y el área del cuadrilátero AOBE. 14) Demostrar que el área del triángulo equilátero de lado a es igual a la suma de las áreas de los triángulos equiláteros de lados b y c. 15) Demostrar que el área del semicírculo de diámetro a es igual a la suma de las áreas de los semicírculos de diámetros b y c.

MATEMATICA III 3º SOCIAL ECONOMIA - ACTIVIDAD 1

MATEMÁTICA III 3º SOCIAL ECONOMIA - ACTIVIDAD Nº 1

1) Construir la matriz 3x2 que tiene:

y los demás elementos cero.

2) Construir la matriz 2x4 cuyo elementos son: Establecer en cada caso si la matriz puede construirse en el Conjunto de los Naturales, en el de los Enteros o en el de los Racionales.

3) Calcular:
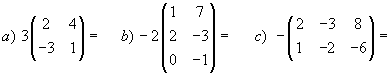4) Calcular: 5) Calcular:
6) Encontrar: x , y , z, w si: 7) Sean las matrices: Realizar la única suma, las 2 sustracciones y los 4 productos posibles entre esas matrices.

8) Sean la matrices: Calcular:
9) Hallar a,b,c y d:
10) La expresión 2(X-3I )+3( X+B) = B+7X donde e I es la matriz identidad, es una ecuación en la incógnita X que es otra matriz. Calcular X.

11) Sea encuentra la matriz X de modo que: a) 3A+2X – I = 0 ; b) A+1/3 (X-I)=2I

12) Si A y B son matrices cuadradas: a) desarrollar A(3A + I)
b) sacar factor común en: 13) Determinar las dos matrices X e Y de modo que se cumplan conjuntamente que: 14) Teniendo en cuenta que
a) Resolver la ecuación en X: 3(X-A) = 2(X+B)

b) Resuelve el sistema en X e Y:

MATEMATICA IV 3º MATEMATICA y DISEÑO: ACTIVIDAD 1

MATEMATICA IV: 3º MATEMÁTICA Y DISEÑO (Reformulación 2006)
ACTIVIDAD No. 1: GEOMETRÍA DEL ESPACIO – Prof. Guillermo R. Osorio Salorio

1) a) Si se multiplica la medida de la arista de un Cubo por dos ¿ por qué número queda multiplicado el volumen?
b) Idem si se multiplica la medida de las aristas por tres.
c) Idem si se multiplica por diez.
d) Idem si se divide por diez.

2) a) Una caja de 25 cm de largo, 15 cm de altura y 10 cm de amcho ¿puede ser llenada por un número entero de cubos de 5 cm de arista? justificar la respuesta.
b) Buscar el error del siguiente razonamiento: “En el interior de una caja cuyas dimensiones son; 15 cm, 25 cm y 8 cm se pueden colocar 24 cubos de 5 cm de arista. En efecto, el volumen de la caja es: (15.25.8) cm3 = 3000 cm3 , el volumen de un cubo de 5 cm de arista es 125 cm3 y tenemos que 3000 : 125 = 24

3) Un invernáculo tiene la forma y dimensiones representadas en la figura. Calcular su volumen.

4) Una torre tiene la forma indicada en la figura adjunta; la altura del cilindro es de 7 m, AO = 3m y SO = 4 m. Calcular el área exterior y el volumen de la torre.

5) ABCDEFGH es un cubo de 3 cm de arista y los segmentos HI, HJ y HK son de 1,5 cm. Construir en verdadera magnitud el desarrollo del poliedro ABCDEFGIJK y calcular el área y volumen de dicho poliedro.

6) Sea un cubo de 4 cm de arista. Los puntos A, B, C, D, E y F señalados en la figura son puntos medios de aristas. El plano que los contiene corta al cubo determinando dos poliedros.
a) Construir en verdadera magnitud el desarrollo de uno de esos poliedros.
b) Calcular área total y volumen del mismo.

MATEMATICA II 3º FISICO MATEMATICO:EJERCICIOS DE REPASO

Matematica II 3º Fisico Matematico Repaso

View more Microsoft Word documents from Guillermo Osorio.

MATEMATICA II 3º FISICO MATEMATICO: ANGULOS (Revisión)

ANGULOS: Definiciones y propiedades

(tomado del libro de Fernández Val)

EJERCICIOS:
1) Sea una circunferencia C de centro O, y en ella un triángulo equilátero inscrito ABC. Se considera un punto exterior P, tal que los segmentos PC y PA cortan a C en C’ y A’ respectivamente, y el ángulo CPA=38º. Deducir el ángulo C'OA.

2) En una circunferencia de centro O se consideran tres puntos: A, B y T, tal que el ángulo BOT= a y el ángulo AOB= 2a . Por T se traza la tangente que corta a la recta AB en P. Hallar en función de "a" todos los ángulos del triángulo APT

3) Se considera un triángulo OAB con el ángulo O=45º . Por un punto M del lado AB, se traza una recta (r) que corta a la recta OA en P y a OB en Q. Sean C y C’ las circunferencias determinadas por los puntos A, M y P, y por B,M y Q respectivamente. Sea N el otro punto de intersección entre C y C’, probar que el ángulo BNA=135º.

MATEMATICA II 3º FISICO MATEMATICO: Resolución de Problemas

RESOLUCION DE PROBLEMAS GEOMÉTRICOS:
En la resolución de un problema geométrico conviene distinguir las siguientes partes:
a) El análisis
b) La Construcción
c) La Demostración
d) La Discusión

En el Análisis se supone el problema resuelto, dibujando una figura que satisfaga aproximadamente las condiciones dadas y se investigan las relaciones existentes entre los elementos conocidos y desconocidos de la misma. Para ello se trazan ciertas líneas adicionales, se divide la figura en partes, se halla la suma o diferencia de algunos elementos, etc., hasta encontrar una serie de propiedades que permitan ir reduciendo el problema a otros más sencillos o ya conocidos.
(Se sigue así un proceso de aplicación general denominado método reductivo el cual consiste en ir transformando el problema propuesto en otros más sencillos hasta llegar a uno que se sepa resolver.)
Es conveniente dibujar varias figuras en posiciones diferentes para evitar el error o la falta de generalidad a que podría conducirnos el haber partido de una posición particular, debiendo hacerse un examen de las condiciones impuestas en el problema para investigar todas las posibles posiciones de la figura que se busca. Este estudio previo de los diferentes casos que pueden presentarse es llamado por algunos autores la discusión del planteamiento.

En la Construcción se hace el dibujo de la figura pedida teniendo para ello en cuenta los resultados y relaciones obtenidos en el análisis del problema.
La construcción se efectúa generalmente utilizando como instrumentos auxiliares la regla y el compás, pero no nos restringiremos al uso exclusivo de estos instrumentos pues tal restricción implica la imposibilidad de resolver en general ciertos problemas sencillísimos, como el de la trisección del ángulo.
En la geometría moderna se propende al empleo, en la resolución de cada problema, del instrumento o instrumentos más adecuados al mismo, sin imponerse previamente limitaciones de ninguna clase. Otra tendencia que se ha manifestado en la Geometría moderna es la de la resolución de los problemas con la menor cantidad posible de instrumentos diferentes.
Las figuras usadas en el análisis del problema son esquemáticas y por consiguiente, de dimensiones arbitrarias. En la construcción, por el contrario, debe darse ala figura las dimensiones requeridas partiendo del verdadero tamaño (o posición) de los datos.
Es recomendable efectuar todas las construcciones auxiliares en la misma figura, siempre que esto no la haga confusa o poco precisa; en este último caso será preferible desarrollar en lugar aparte algunas de dichas construcciones auxiliares o intermedias.
Una construcción se considera tanto más elegante cuanto menos líneas auxiliares y teoremas geométricos se hagan intervenir en ella; y también, cuánto más simples sean los instrumentos empleados en la misma. Deberá procurarse pues, la construcción más económica, comprendiendo en este concepto no solamente la economía de pensamiento sino también ciertas economías de trabajo.
En la construcción de la figura deben observarse las reglas generales del dibujo lineal y, en particular, los convenios siguientes: los datos se dibujan con línea llena y fina, las líneas auxiliares se hacen de trazos, de puntos, o de trazos y puntos (según convenga), o líneas muy finas, y los resultados se dibujan con línea llena y gruesa (o con algún lápiz de bello color).

En la Demostración se justifica la construcción realizada probando que la figura obtenida satisface las condiciones del problema. Como en la demostración se sigue, en general, el proceso inverso al utilizado en el análisis, se necesitará, para que esta justificación sea válida, que sean ciertos los teoremas recíprocos de los que intervinieron en el análisis.

En la Discusión se estudian: a) los casos de posibilidad o imposibilidad del problema; b) los casos de determinación o indeterminación del mismo; c) los casos particulares interesantes que pueda ofrecer.

Métodos de resolución de los problemas geométricos.

Hoy en día, gracias a la sistematización lograda en la Geometría, mediante la introducción de ciertos conceptos generales como los de lugar geométrico, transformación geométrica y sistemas de coordenadas, es posible llegar mediante una reflexión metódica, es decir, por medio de un estudio sistemáticamente conducido, a la resolución de la mayoría de los problemas.
Claro es que los factores de habilidad intelectual, buen discernimiento y conocimientos previos asimilados mantendrán siempre importancia preponderante. En cuanto a la necesidad de hallarse plenamente familiarizado con la mayor cantidad posible de propiedades geométricas, resulta evidente, pues existen teoremas muy fecundos que proporcionan la clave para la resolución en gran número de casos.
Los métodos de resolución de los problemas geométricos los clasificaremos en la siguiente forma:
1) Método de los Lugares Geométricos
2) Método de transformación de la figura
3) Método algebraico.

El método de los Lugares Geométricos consiste esencialmente en prescindir de alguna o algunas de las condiciones del problema, sustituyéndolo por otros problemas indeterminados pero más simples. Se obtienen entonces varios lugares geométricos de cuya combinación o intersección resulta la solución del problema propuesto.

El método de Transformación de la figura consiste como su nombre lo indica, en someter la figura o una parte de ella a una transformación que facilite la resolución del problema o que lo transforme en otro más sencillo. Según el tipo de transformación geométrica usado se tienen diferentes métodos especiales que estudiaremos sucesivamente, a saber: traslación, rotación, simetría, homotecia y semejanza.
El método algebraico consiste en expresar mediante una fórmula algún elemento geométrico (por ejemplo un segmento) cuya determinación permita resolver el problema fácilmente. Ello se logra relacionando algebraicamente los datos con algunos elementos desconocidos (mediante los teoremas que expresan relaciones métricas en el triángulo, en los polígonos, en el círculo, etc, o bien, con auxilio de la geometría analítica) y resolviendo las ecuaciones resultantes con respecto a las incógnitas correspondientes a dichos elementos. Por último se efectúan geométricamente las operaciones indicadas por la fórmula obtenida.
En este método puede recurrirse, si es necesario, al uso de relaciones trigonométricas.

NORMAS GENERALES SOBRE LAS DEMOSTRACIONES Y RESOLUCIÓN DE PROBLEMAS ( Mario Coppetti – Geometría Racional 2do.año)
Los desarrollos de muchos teoremas y problemas geométricos, tienen ciertas analogías que conviene destacar, porque forman un conjunto de normas generales que, de tenerlas presentes, facilitan las demostraciones y resolución de problemas.
Dada la variedad de cuestiones geométricas que se pueden proponer, es imposible indicar un método general para la resolución de todos los problemas de Geometría, pero sí, algunas normas generales, aplicables a cuestiones de índole análoga.
Para resolver un problema de Geometría, o demostrar una propiedad de las figuras geométricas, es conveniente:
1) establecer concretamente el objeto del problema o de la propiedad.
2) Establecer claramente cuál es la Hipótesis y cuál es la Tesis.
3) Construir una figura geométrica que corresponda al enunciado del problema o de la propiedad, marcando en ella la hipótesis y la tesis.
4) Si la tesis requiere un dibujo algo complicado, dibujar primeramente una figura que se aproxime lo más que sea posible a la tesis, llamada figura de análisis. Del estudio de esta figura podrá deducirse, generalmente, la construcción necesaria para llegar rigurosamente a la tesis. Esto se logra deduciendo de la hipótesis del problema todas las consecuencias posibles y convenientes, recordando las propiedades de las figuras que constituyen el objeto del problema o de la propiedad a demostrar.
5) Demostrada la tesis, conviene verificar si la solución es general, dentro de la hipótesis del problema o de la propiedad; o bien, si se presentan casos particulares, en los que el problema no tiene solución; esto constituye la discusión del problema.
6) a) Para demostrar la igualdad de segmentos, trátese de demostrar que son lados homólogos de triángulos iguales o lados de un triángulo isósceles, o lados opuestos de un paralelogramo, etc.
b) Para demostrar la igualdad de dos ángulos, trátese de demostrar que son ángulos correspondientes o alternos internos entre paralelas, o que tienen los lados paralelos o perpendiculares, o que son ángulos homólogos de triángulos iguales, o suplementos o complementos de un mismo ángulo, o adyacentes a la base de un triángulo isósceles, u opuestos de un paralelogramo, o que tienen la misma medida, o que son la suma o diferencia de ángulos iguales, etc.
a) Para demostrar que un ángulo es mayor que otro, véase sui es opuesto a mayor lado que el otro en el mismo triángulo, o si es externo de un triángulo, etc.
b) Para demostrar que un segmento es mayor que otro, véase si se opone a mayor ángulo en un triángulo, o si es un segmento oblicuo que tenga mayor proyección que el otro, etc.
c) Para demostrar que dos rectas son perpendiculares, empléense las propiedades de los triángulos isósceles o rectángulos, o las de las bisectrices de ángulos suplementarios, o las del rombo o del cuadrado, etc.
d) Para demostrar que dos rectas son paralelas, empléense las propiedades de los ángulos determinados por una secante a dos rectas, o las propiedades del paralelogramo, etc.

MATEMATICA II 3º FISICO MATEMATICO Introducción

Matematica II 3º Fisico Matematica Actividad Introductoria Al Curso

View more Microsoft Word documents from guest1c433c.

FELIZ COMIENZO DE CURSOS 2009

Hola a todos!!! simplemente para desearles un muy buen año lectivo 2009 y que a través de este Blog estaremos en contacto permanente para evacuar dudas y aportar el material necesario para los distintos cursos. Espero que juntos podamos lograr nuestros objetivos y cumplir nuestras metas. Recuerden que lo más importante es aprender para seguir creciendo y superarse como estudiantes y como personas para ser cada día mejores ciudadanos.
Prof. Guillermo Osorio Salorio